Rlc Circuit Read Voltage High Pass Low Pass
Introduction: Passive Filter Circuits
This instructable is intended to show you how to brand several different filter circuits, in particular, low pass and high pass filters, along with a give-and-take of notch/trap filters and bandpass filters.
What are Filters?
And so what is a filter and why would you ever want to build one? Well, you might not cease up building any of these circuits by themselves, but you may detect yourself integrating them into more complex circuits. Yous already know what everyday filters practice (eastward.m. air filters, h2o filters); electronic filters are no different. They accept some signal, which in this case is a voltage signal composed of ane or many frequencies, and filter out frequencies in a specific range.
High and Low Pass Filters
High laissez passer filters are circuits used to remove depression frequency signals and allow loftier frequency signals. Low pass filters do the contrary and are used to remove high frequency signals and allow through low frequency signals.
Applications
High laissez passer filters are oft used in speakers to filter out bass from an audio signal being sent to a tweeter, which could be damaged by the low frequency bass signals. They are also used to remove DC get-go or DC bias from a signal, which could otherwise harm amplifiers and other electronic devices. In contrast, depression pass filters tin can be used to filter out high frequency signals in sound being sent to subwoofers that can't efficiently reproduce the high-frequency parts of the audio signal. They are likewise used in devices such every bit in the tone knob of an electric guitar (to filter out treble), or in analog synthesizers.
Other Filters
Two other filter circuits that we will briefly talk over are the notch and bandpass filters. Notch filters are used to filter out a very specific range of frequencies, for example to filter out interference of a particular frequency if yous happen to live side by side to a radio station. Bandpass filters exercise the reverse and will filter out everything just frequencies in a narrow range, and are thus used in radios to tune in to a specific frequency.
Stride 1: The High Pass Filter
What Y'all Need
What you put into the circuit:
- One capacitor with capacitance C (in F).
- I resistor with resistance R (in Ω).
- An input signal (ours came from a function generator).
- An oscilloscope (for testing).
What you lot leave of the circuit:
- A filtered output indicate.
How to Build the Circuit
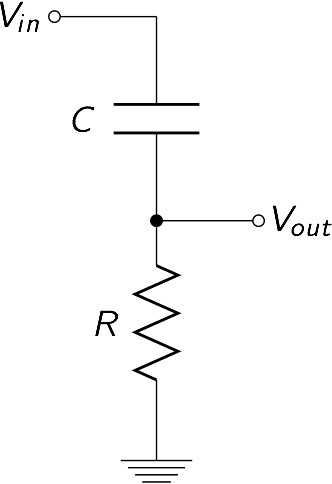
Where practise the parts get?
Your input betoken is first fed into a capacitor that is connected at its other end to a resistor, which in plough is continued at its other end to ground. Your output betoken should be read betwixt the capacitor and resistor.
Examination to make certain it works.
If yous don't have admission to a function generator or oscilloscope, you'll have to trust we tested the circuit for yous correctly. We congenital our excursion as shown:

The red alligator clip carries our input signal (from a function generator), the black alligator clip atomic number 82 to ground, and the green wire carries our output point, which nosotros sent to an oscilloscope for testing. As we went from low frequency signals to high frequency signals, the result we read on our oscilloscope looked like this:

The yellow bend is our input signal, and the blue curve is our output point (note that while the yellowish curve appears to remain the same, it is considering we were irresolute the frequency scaling on the brandish of the oscilloscope). At low frequencies, you tin can see that the entire signal is filtered out and we go almost no output indicate. As frequency increases, the output point becomes larger, until it reaches a point at which it is virtually the same as the input signal. This point is called the cutoff frequency, and we will testify you how to find it afterward. Y'all should also note that the output signal can be phase-shifted from the original input point, significant that although the signals take the same frequency, they aren't necessarily "in step", so to speak.
Also, note that while we intentionally inputted signals of a uniform frequency at a time, the excursion volition work for chemical compound signals.
The Cutoff Frequency
Calculate the cutoff frequency.
The cutoff frequency is generally considered the frequency at which the signal is attenuated (or filtered). This means that whatsoever betoken with frequency below the cutoff frequency is considered to be filtered, and any point with frequency above the cutoff is considered to be "left alone" or unfiltered. So what is the cutoff frequency?

where R is the resistance of your resistor in Ω and C is the capacitance of your capacitor in F.
What does the cutoff frequency mean for the signal?
If y'all have a wait at the ratio of the amplitude of the output betoken to the amplitude of the input bespeak over a broad range of frequencies, you will get something that looks as and so

Note that both axes are log-scaled. This means essentially that if you move up from one light gray line to the next, your value is actually increasing past 10 times. This means that if y'all looked at this plot without log scaled axes, you would substantially run across an almost vertical driblet off at the cutoff frequency. Whatsoever indicate or component of a signal that has frequency higher than the cutoff frequency, still, is unfiltered, to a skillful approximation.
The output point is phase shifted from the input.
Nosotros said before that the input and output signals are not "in step" and are actually shifted. This may be fine for some applications, but there are other applications where this may be of import. The phase shift changes as the frequency of the input signal changes, but every bit with the gain, and the plot of this modify looks as so

At low frequencies, the output signal is phase shifted past π/two, and at loftier frequencies the stage shift is almost zero. The cutoff frequency is important to the phase shift because it is the frequency at which the output betoken is phase shifted past exactly half of π/2, or π/4.
BUT HOW DID YOU GET THESE RESULTS?!?!
If you really want to know, get bank check out the Theory section for more than data nigh how the circuit works and how we calculated the proceeds and phase shift.
TL;DR
- The high pass filter can be made every bit follows:
- Input - Capacitor - (Output) - Resistor - Footing
- Loftier pass filters filter out signal with frequencies below the cutoff frequency (1/2πRC).
- Since the cutoff is strictly determined past R and C, choose the appropriate resistor and capacitor to cutoff frequencies where you want to
- The output point is phase shifted from the input.
Step 2: The Low Pass Filter
This section will exist similar in content to the department on the high pass filter, so if you lot've already read that, much of the information establish there volition utilize to low pass filters as well, except with well-nigh everything flipped effectually.
What Yous Need
What you put into the circuit:
- One capacitor with capacitance C (in F).
- One resistor with resistance R (in Ω).
- An input betoken (ours came from a function generator).
- An oscilloscope (for testing).
What you lot exit of the circuit:
- A filtered output signal.
How to Build the Circuit

Where do the parts get?
Your input betoken is beginning fed into a resistor that is connected at its other end to a capacitor, which in turn is connected at its other terminate to ground. Your output betoken should be read betwixt the resistor and capacitor.
Test to make sure it works.
If you don't have access to a part generator or oscilloscope, you'll have to trust we tested the circuit for y'all correctly. Nosotros built our circuit as shown:

The scarlet alligator clip carries our input signal (from a function generator), the black alligator prune lead to ground, and the green wire carries our output signal, which we sent to an oscilloscope for testing. Equally we went from low frequency signals to high frequency signals, the result we read on our oscilloscope looked similar this:

The yellow curve is our input point, and the blueish curve is our output signal (notation that while the yellowish curve appears to remain the aforementioned, it is because we were changing the frequency scaling on the brandish of the oscilloscope). At low frequencies, you lot tin can see that near none of the signal is filtered and our output is well-nigh identical to our input. When the frequency reaches the cutoff frequency, the output indicate starts getting noticeably smaller than the input point. From hither, as frequency increases, the output signal grows smaller and smaller, until almost no signal is left. You should as well annotation that the output bespeak can be phase-shifted from the original input bespeak, meaning that although the signals have the same frequency, they aren't necessarily "in footstep", so to speak.
Also, annotation that while we intentionally inputted signals of a uniform frequency at a time, the circuit will work for compound signals.
The Cutoff Frequency
Summate the cutoff frequency.
The cutoff frequency is generally considered the frequency at which the signal is attenuated (or filtered). This means that any signal with frequency above the cutoff frequency is considered to be filtered, and any indicate with frequency below the cutoff is considered to exist "left alone" or unfiltered. So what is the cutoff frequency?

where R is the resistance of your resistor in Ω and C is the capacitance of your capacitor in F.
What does the cutoff frequency mean for the signal?
If you accept a look at the ratio of the amplitude of the output bespeak to the amplitude of the input signal over a broad range of frequencies, you volition get something that looks every bit so

Note that both axes are log-scaled. This ways essentially that if you move up from one light gray line to the next, your value is actually increasing by 10 times. This means that if you looked at this plot without log scaled axes, you would substantially see an almost vertical drop off at the cutoff frequency. Any signal or component of a signal that has frequency lower than the cutoff frequency, notwithstanding, is unfiltered, to a practiced approximation.
The output betoken is phase shifted from the input.
We said before that the input and output signals are not "in step" and are actually shifted. This may be fine for some applications, but there are other applications where this may be important. The phase shift changes equally the frequency of the input signal changes, just every bit with the gain, and the plot of this change looks as so

At depression frequencies, the output signal is phase shifted past zero, and at high frequencies the phase shift is almost π/2. The cutoff frequency is of import to the stage shift because it is the frequency at which the output signal is phase shifted by exactly one-half of π/2, or π/four.
BUT HOW DID Yous GET THESE RESULTS?!?!
If you lot really want to know, go bank check out the Theory section for more than information about how the circuit works and how nosotros calculated the gain and stage shift.
TL;DR
- The depression laissez passer filter can be made as follows:
- Input - Resistor - (Output) - Capacitor - Basis
- Depression pass filters filter out betoken with frequencies above the cutoff frequency (1/2πRC).
- Since the cutoff is strictly adamant by R and C, choose the advisable resistor and capacitor to cutoff frequencies where y'all want to
- The output point is stage shifted from the input.
Pace three: The Bandstop and Bandpass Filters
Nosotros volition only briefly hash out notch filters and bandpass filters here. These are only the most basic versions of such filters, and thus will only serve the most basic of needs.
Notch/Trap/Bandstop Filter
What is it?
A bandstop filter is a circuit that ideally filters out signals with frequencies in a certain range. This range can be quite large, depending on inherent characteristics of the circuit. The smaller the range of frequencies the circuit filters, the college the Q factor it is said to have. Bandstop filters with high Q factors are also called notch filters.
Build a simple notch filter.
Using a resistor, a capacitor, and an inductor, you tin build a elementary notch filter as follows:

What frequencies does it filter?
The center frequency, likewise called the resonant frequency, effectually which this circuit will filter can exist institute equally

where L is the inductance of the inductor in H, and C is the capacitance of the capacitor in F.
Bandpass Filter
What is it?
A bandpass filter is a circuit that ideally filters out signals of all frequencies except those in a certain range. This range can exist quite large, depending on inherent characteristics of the circuit. The smaller the range of frequencies the excursion allows through, the higher the Q gene it is said to accept.
Build a simple bandpass filter.
Using a resistor, a capacitor, and an inductor, you can build a simple bandpass filter equally follows:

What frequencies does it allow through?
The eye frequency, or resonant frequency, around which the circuit will permit passage can be institute similarly every bit

where Fifty is the inductance of the inductor in H, and C is the capacitance of the capacitor in F.
Footstep 4: The Theory Behind the Filter Circuits
Epitome from xkcd.com.
This step is here only to indulge your scientific curiosity and is, by no means, necessary in order to build useful filter circuits.
Voltage Dividers
What is a voltage divider?
A voltage divider, as its proper name suggests, is a circuit that takes in an input voltage and puts out an output voltage that is equal to some fraction of the input voltage. The circuit itself is simply a voltage source connected to two resistors in series, with the output betwixt the two resistors equally shown below.

How does this circuit work?

The key to agreement how the voltage divider works is knowing that the current, I, should be equal across both resistors if in that location is no current being drawn at the output. Using Ohm's Law (Five=IR, Voltage = Electric current 10 Resistance), we see that the voltage drop beyond each of the two resistors is proportional to its resistance. For instance, the input voltage is carve up evenly across both resistors if the resistors take the aforementioned resistances. To put it some other way (and really get a formula for the output voltage) let's calculate the circuit'due south current in terms of the input voltage and total resistance using Ohm's police force.

Now calculate the circuit's current in terms of the output voltage, once more using Ohm's law.

The voltage drop beyond the 2nd resistor is equal to the output voltage. Note that these 2 currents are equal, as we said earlier, so we tin set the ii equations equal to one another and solve for the output voltage.

This shows that the output voltage is adamant past the ratio of the resistance of the second resistor to the total resistance of the two resistors.
A quick example

A Capacitor's Impedance
Every bit y'all may accept noticed, our loftier pass and low pass filters were merely voltage dividers with ane of the resistors replaced with a capacitor. Therefore, we tin can theoretically do the same analysis as to a higher place to find out how our filters work, simply showtime we need to understand impedances.
You tin can think of impedance as a generalized resistance. For instance the impedance of a resistor is called resistance, as you know. The impedance of a resistor is simply R, the value of the resistance, but what is the impedance of a capacitor? Well capacitors take impedances that are represented by a complex value, 1/(jωC) where C is the Capacitance of the capacitor, ω is frequency of the signal passing through the capacitor in radians (ω=2πf, where f is frequency in Hertz), and j is just the imaginary number i=√-1, (we use j instead of i so we don't misfile it with current).
Notice that the capacitor's impedance is frequency dependent. For frequencies close to zilch the impedance of a capacitor goes to infinity, however, for very high frequencies the impedance goes to zip. In other words, the impedance of a capacitor looks like a big resistor at low frequencies and like a uncomplicated wire with no resistance at high frequencies.
Understanding the High Pass and Depression Pass Circuits
You call back the equation that determines a voltage divider's output,

If we generalized this for impedances nosotros become something similar

where Z is just the impedance of our circuit elements, and the tildes or squiggly lines simply mean that we are dealing with complex numbers. For a depression laissez passer filter we have a resistor at the top and a capacitor at the bottom and then

That's kind of nasty looking but if we simplify we get

Not too bad right?
This concluding formula is fundamental to understanding why the low laissez passer filter only filters high frequencies. Notice that for low frequencies jωRC is approximately zero and then the output voltage approximately equals the input voltage. Now for high frequencies jωRC is approximately space so we get that the output voltage is almost zilch. See how this works? When our complex voltage (fabricated upwards of various waves with different frequencies) serves as the input voltage for our filter, the high frequency parts of the voltage create an output voltage equal to zero while the low frequency parts create an output voltage equal to the input voltage (i.e. nosotros only go the low frequency part of our signal dorsum).
The same argument we applied to depression laissez passer filters can be used on high laissez passer filters, simply switch the location of the resistor and the capacitor. We yet use the same formula

However, this time

If nosotros simplify we should get

Once again, for high frequencies we basically become jωRC ≈ jωRC + 1 so nosotros should get an output voltage equal to our input voltage. For low frequencies nosotros get jωRC ≈ 0 so the output voltage is well-nigh zero. Equally you can meet, as promised nosotros passed over our high frequencies and merely filtered out the low frequency.
Cutoff Frequency
As mentioned earlier, the cutoff frequency is a very important value to know for a high pass or low pass filter circuit. How do we actually find it though? The cutoff frequency is defined as the frequency at which the output voltage is exactly 1/√two of the input voltage. This is the point at which the filter starts the benumb the input bespeak. If you solved for this frequency using our equations to a higher place, yous would find

where ω = 2πf. As you can run into, the cutoff frequency is determined strictly past the values nosotros cull for our resistance and capacitance, therefore we can choose exactly where we want our circuit to start filtering signals.
Be the First to Share
Recommendations
Source: https://www.instructables.com/Passive-Filter-Circuits/
ارسال یک نظر for "Rlc Circuit Read Voltage High Pass Low Pass"